- 1 关于禅道效能分析
- 2. X分析的维护管理
- 2.1. 分析项目管理
- 2.2. 分析报告
- 3. 分析方法
- 3.1 五类分析方法介绍
- 3.2. 图形
- 3.2.1 箱线图
- 3.3. 相关与回归
- 3.3.1 相关性
- 3.3.2 回归拟合图
- 3.3.3 线性回归
- 3.3.4 多次方程回归
- 3.3.5 Gompertz模型
- 3.3.2 回归拟合图
- 3.4. 控制图
- 3.4.1 I-MR控制图
- 3.5. 假设检验
- 3.5.1 正态性检验
- 3.6. 统计
- 3.2. 图形
- 4. 执行核心对象数据分析
- 4.1 执行任务列表工时分析
- 4.2 执行需求列表效率分析
- 4.3 执行需求列表变更分析
- 4.4 执行Bug列表重开分析
- 4.5 执行用例列表效率分析
- 4.6 执行用例列表效果分析
- 4.2 执行需求列表效率分析
- 2. X分析的维护管理
正态性检验 分享链接
在企业的数据分析领域,各种复杂的模型和算法常常备受瞩目,仿佛掌握了它们就能解锁数据宝藏的密码。然而,有一个看似基础却至关重要的环节常常被人们忽视,那就是正态性检验。或许你还记得高中老师曾提及的这个概念,今天就让我们深入探讨一下它在企业数据分析中的重要意义。
什么是正态性检验?
正态分布,也被称为高斯分布,是一种在自然界和社会现象中广泛存在的概率分布。它的形状像一口钟,中间高,两边低,左右对称。而正态性检验,就是判断一组数据是否服从正态分布的过程。若随机变量X服从一个平均数为μ、标准差为σ的正态分布,则记为:X~N(μ,σ^2)- μ决定了分布的位置
- σ决定了分布的幅度
为什么要进行正态性检验?
确保分析方法的适用性:许多常用的统计方法(如 t 检验、方差分析、回归分析等)都建立在数据服从正态分布的假设基础之上。当数据不满足正态分布时,这些方法的理论依据便不再成立。
识别异常或特殊分布:正态性检验可以帮助我们发现数据中的异常值或特殊分布(如偏态、峰态)。这些信息对深入分析问题原因、优化流程至关重要。
提高决策的科学性:在质量管理、业务分析等领域,正态分布是许多关键指标(如缺陷率、响应时间、成本等)的常见分布形态,通过正态性检验,我们可以更准确地理解数据的特性,从而制定更科学的改进措施。
支持预测模型的准确性:在回归分析等预测模型中,正态分布的残差是模型有效性的重要假设之一。正态性检验可以验证这一假设是否整理,确保预测结果可靠。
如何进行正态性检验?
1.图形法:通过绘制直方图、正态概率图等图形来直观地判断数据是否服从正态分布。
直方图可以展示数据的分布形状,若数据服从正态分布,直方图呈现为钟形。
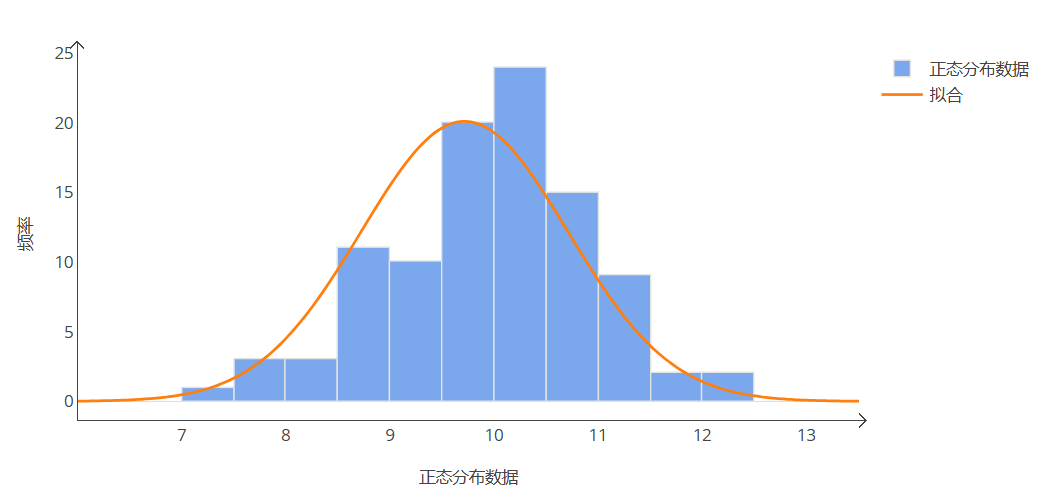
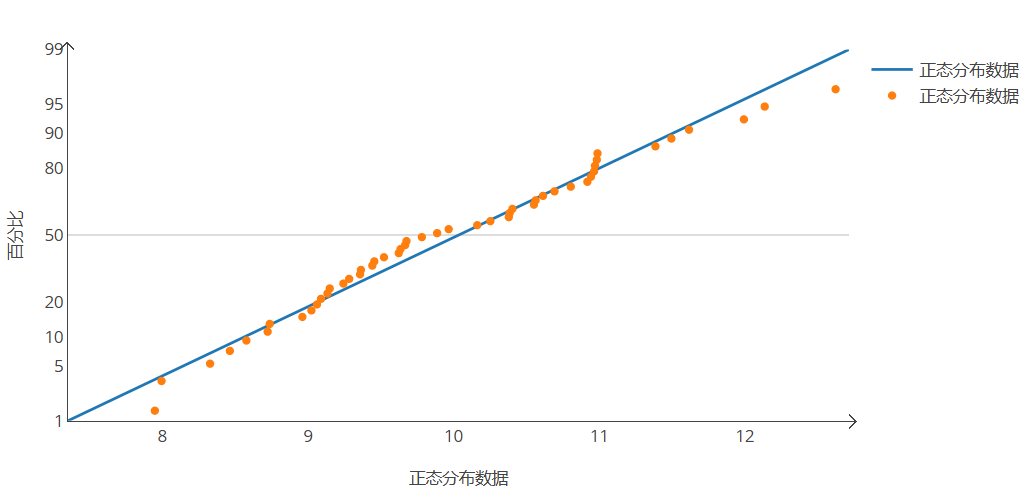
正态概率图则是将数据的分位数与理论正态分布的分位数进行比较,如果数据点大致落在一条直线上,说明数据可能服从正态分布。
2.统计检验法:常用的统计检验方法有Anderson-Darling、Ryan-Joiner、Kolmogorov-Smirnova。
Anderson-Darling检验:对于小样本和大样本都适用,并且在处理小样本时也能较好地检测出与正态分布的偏离,不过对于大样本,它对偏离的检测会更加敏感。
- Ryan-Joiner检验:通常更适用于小样本数据(一般样本量小于 20 时效果较好)。在小样本情况下,它能够比较有效地判断数据是否来自正态总体,但随着样本量的增大,其检验效能可能会有所下降。
- Kolmogorov-Smirnov检验:在小样本时,该检验比较常用且有一定的效果,但当样本量较大时,检验可能会过于敏感,即使数据与正态分布的偏离非常小(在实际应用中可能并不重要),也可能会拒绝原假设,得出数据不服从正态分布的结论。
使用ZenDAS进行正态性检验
方法一:正态性检验
step1:在ZenDAS中选择正态性检验分析方法
step2:填写正态性检验的表单
选择要检验的数据
选择检验使用的方法
设置想要查看的X轴数据的或Y轴百分数所在的位置
step3:查看分析结果
p值>0.05符合正态性检验
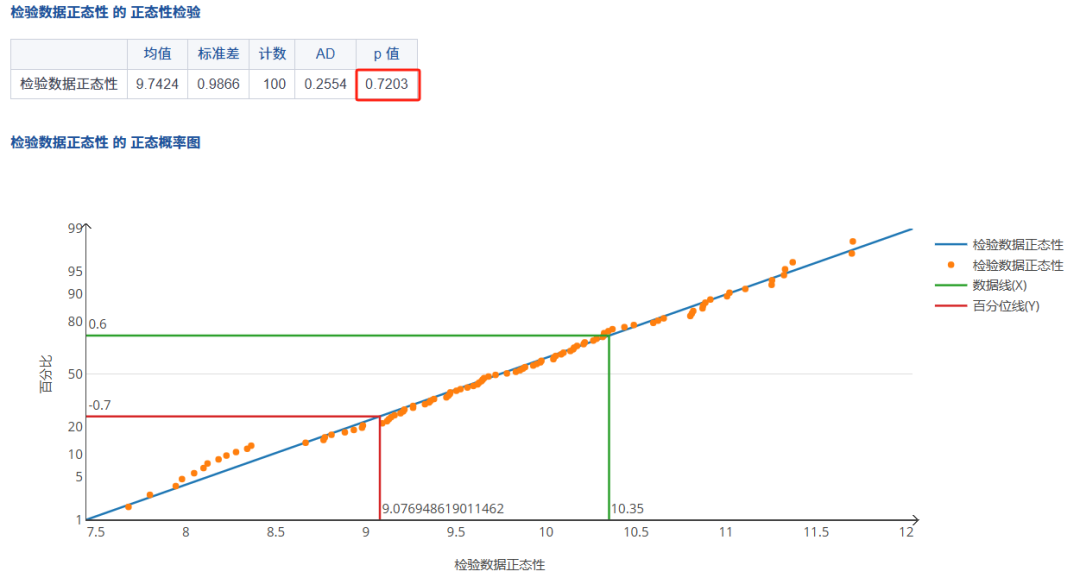
方法二:图形化汇总
step1:在X分析中选择图形化汇总分析方法
step2:填写图形化汇总的表单
选择要检验的数据
选择要查看的数据
选择要查看的图形
step3:查看分析结果
p值>0.05符合正态性检验
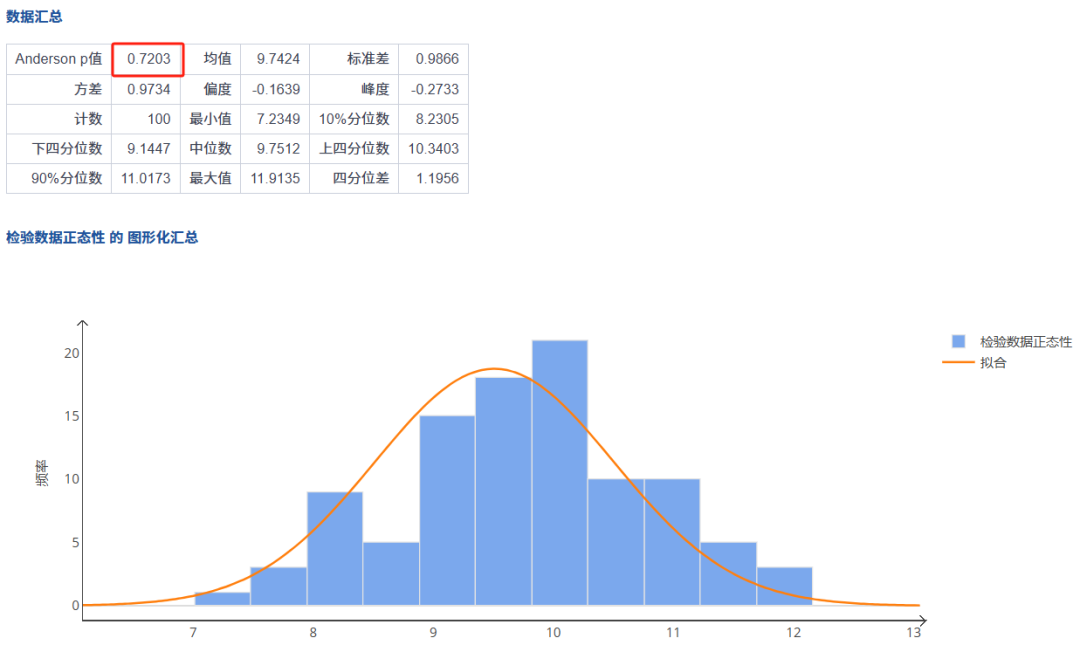








 精品资料包
精品资料包 1V1产品演示
1V1产品演示 免费试用增强功能
免费试用增强功能 专属顾问答疑支持
专属顾问答疑支持


